Concept of REDSHIFT is one of the important subjects that one should know to understand the universe. It helps one's brain to identify whether our universe is expanding, compressing, or it is stationary. So, this post is just to give you the basic idea of the redshift theory.
Cosmological (metagalactic) red shift. The observed decrease in the radiation frequencies of all distant sources (galaxies, quasars), indicating that these sources are receding from each other and, in particular, from our galaxy, and that the universe is nonstationary (expanding), is called cosmological (metagalactic) red shift. Cosmological red shifts were discovered for galaxies by the American astronomer V. Slipher in 1912–14. In 1929, E. Hubble discovered that the red shift for distant galaxies was greater than for near galaxies and increases nearly proportionally with distance (law of red shifts, or Hubble’s law).
Different explanations have been proposed for the observed shift of the spectral lines. One hypothesis states that the light quanta “decay” in the time it takes, amounting to millions and billions of years, for the light from distant sources to reach the observer on the earth. According to this hypothesis, the energy decreases during the decay, and the change in the radiation frequency is related to this. This hypothesis, however, has not been confirmed by observation. In particular, the red shift in different regions of the spectrum from the same source must, within the framework of the hypothesis, be different. On the other hand, all observational data indicate that the red shift is independent of frequency and that the relative change of freqencyz = (f0 – f)/f0 is identical for all radiation frequencies not only in the optical band but also in the radio-frequency band of a given source (f0 is the frequency of a line in the spectrum of the source, f is the frequency of the same line as recorded by a detector, and f < f0). This change of frequency is a characteristic property of the Doppler shift and in fact excludes all other interpretations of the red shift.
In the theory of relativity, the red shift is viewed as the result of time dilatation in a moving frame of reference (an effect of the special theory of relativity). If the velocity of the frame of the source relative to the frame of the detector is ν (in the case of metagalactic red shift, ν is the radial velocity), then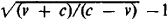
, where c is the velocity of light in a vacuum. It is easy to determine the radial velocity of the source from the observed red shift:
![]()
It follows from this equation that as z → ∞, the velocity ν approaches the velocity of light but always remains less than this speed (v < c). At a velocity ν much less than the speed of light (v ≪ c), the formula is simplified: ν ≈ cz. Hubble’s law in this case is written in the form ν = cz = Hr, where r is the distance and H is Hubble’s constant. The numerical value of H must be known in order to determine distances to extragalactic objects. Knowledge of this constant is also important for cosmology, since the age of the universe is connected with it.
Extragalactic distances (the measurement of which is extremely difficult) were greatly understated prior to the 1950’s, so that the value of H determined from these distances was greatly overestimated. In the early 1970’s, values of 53 ± 5 (km/sec) Mparsecs for Hubble’s constant H and T = 1/H = 18 × 109 years for the reciprocal have been accepted.
Photographing the spectra of weak (distant) sources to measure red shifts requires favorable observing conditions and lengthy exposure times even with the use of the largest telescopes and the most sensitive plates. Shifts of z ≈ 0.2, the corresponding velocities ν ≈ 60,000 km/sec, and a distance greater than 1 billion parsecs have been reliably measured for the galaxies. Hubble’s law at such velocities and distances is used in the simplest form (the error is of the order of 10 percent, that is, the same as the error in determining H). Quasars are on the average 100 times brighter than galaxies and, consequently, can be observed at distances ten times as great (if space is Euclidean). In fact, z ≈ 2 and greater have been recorded for quasars. For shifts of z = 2 the velocity is ν ≈ 0.8 • c = 240,000 km/sec. At such velocities the specific cosmological effects of nonstationariness and space-time curvature are greatly in evidence. In particular, the concept of a unique well-defined distance (one of the distances—the distance obtained from the red shift—is evidently r = v/H = 4.5 billion parsecs) becomes inapplicable here. The red shift attests to the expansion of all parts of the universe accessible to observation. This phenomenon is usually called the expansion of the (astronomical) universe.
Gravitational red shift. Gravitational red shift is a consequence of time dilatation caused by a gravitational field (an effect of the general theory of relativity). This phenomenon (also called the Einstein shift or generalized Doppler effect) was predicted by A. Einstein in 1911 and was first observed in 1919 in solar emission and subsequently in the emission of other stars.
It is customary to characterize the gravitational red shift by a nominal velocity v, formally calculated from the same formulas as in the case of cosmological red shifts. The values of the nominal velocity are ν = 0.6 km/sec for the sun and ν = 20 km/sec for the dense star Sirius B. The red shift caused by the earth’s gravitational field, which proved to be very small (v = 7.5 × 10−5 cm/sec), was first successfully measured in 1959 by the Môssbauer effect. In certain cases (for example, in gravitational collapse), both types of red shift (as additive effects) should be observed
what is red shift?
Imagine you are out for your morning walk when a giant bus comes barreling down the road toward you. As it approaches, the driver lays on his horn and you jump out of the way. The closer the bus gets, the higher the pitch of the horn. As the bus passes, the pitch of the horn becomes lower. This is change in sound as something approaches and recedes is called the Doppler Shift. As the bus moves closer to you, the wavelength of the sound waves is shortening and the frequency of the waves is increasing. As it moves away, the opposite happens: wavelength is increasing and the frequency is decreasing.
The same process that we have observed with sound also happens with light. When an object is emitting light and moving toward you, the light wavelength decreases while the frequency increases, in other words, it gets compressed (or squished). This wavelength corresponds to the blue end of the visual color spectrum. This object is said to be blueshifted. Inversely, when an object is moving away, the wavelength of the light it is emitting increases, while the frequency decreases: it gets stretched out. This corresponds to the red end of the visual color spectrum, and the object is said to be redshifted.
In the 1920's Edwin Hubble was using the concept of redshift and blueshift to calculate the distances of "nebulae" (later known as galaxies). He found that all of the galaxies outside our local group were moving away from each other. For centuries, the Universe had been a static place, and now we knew that it was not only moving, it was expanding! The newfound knowledge of the expanding Universe led directly to the theory of the Big Bang.
In 1917, Albert Einstein had found that his newly developed theory of general relativity indicated that the universe must be either expanding or contracting. Unable to believe what his own equations were telling him, Einstein introduced a cosmological constant (a "fudge factor") to the equations to avoid this "problem". When Einstein heard of Hubble's discovery, he said that changing his equations was "the biggest blunder of [his] life."
much deeper in to red shift:
A decrease in the frequencies of electromagnetic radiation, one of the manifestations of the Doppler effect. The term “red shift” reflects the fact that the lines in the visible region of the spectrum are shifted toward the red end as a result of this phenomenon. Red shift is also observed in radiations at other frequencies, for example, in the radio-frequency band. The opposite effect, that is, an increase in frequencies, is called blue (or violet) shift. The term “red shift” is usually used to denote two phenomena, cosmological red shift and gravitational red shift.
Cosmological (metagalactic) red shift. The observed decrease in the radiation frequencies of all distant sources (galaxies, quasars), indicating that these sources are receding from each other and, in particular, from our galaxy, and that the universe is nonstationary (expanding), is called cosmological (metagalactic) red shift. Cosmological red shifts were discovered for galaxies by the American astronomer V. Slipher in 1912–14. In 1929, E. Hubble discovered that the red shift for distant galaxies was greater than for near galaxies and increases nearly proportionally with distance (law of red shifts, or Hubble’s law).
Different explanations have been proposed for the observed shift of the spectral lines. One hypothesis states that the light quanta “decay” in the time it takes, amounting to millions and billions of years, for the light from distant sources to reach the observer on the earth. According to this hypothesis, the energy decreases during the decay, and the change in the radiation frequency is related to this. This hypothesis, however, has not been confirmed by observation. In particular, the red shift in different regions of the spectrum from the same source must, within the framework of the hypothesis, be different. On the other hand, all observational data indicate that the red shift is independent of frequency and that the relative change of freqencyz = (f0 – f)/f0 is identical for all radiation frequencies not only in the optical band but also in the radio-frequency band of a given source (f0 is the frequency of a line in the spectrum of the source, f is the frequency of the same line as recorded by a detector, and f < f0). This change of frequency is a characteristic property of the Doppler shift and in fact excludes all other interpretations of the red shift.
In the theory of relativity, the red shift is viewed as the result of time dilatation in a moving frame of reference (an effect of the special theory of relativity). If the velocity of the frame of the source relative to the frame of the detector is ν (in the case of metagalactic red shift, ν is the radial velocity), then
, where c is the velocity of light in a vacuum. It is easy to determine the radial velocity of the source from the observed red shift:It follows from this equation that as z → ∞, the velocity ν approaches the velocity of light but always remains less than this speed (v < c). At a velocity ν much less than the speed of light (v ≪ c), the formula is simplified: ν ≈ cz. Hubble’s law in this case is written in the form ν = cz = Hr, where r is the distance and H is Hubble’s constant. The numerical value of H must be known in order to determine distances to extragalactic objects. Knowledge of this constant is also important for cosmology, since the age of the universe is connected with it.
Extragalactic distances (the measurement of which is extremely difficult) were greatly understated prior to the 1950’s, so that the value of H determined from these distances was greatly overestimated. In the early 1970’s, values of 53 ± 5 (km/sec) Mparsecs for Hubble’s constant H and T = 1/H = 18 × 109 years for the reciprocal have been accepted.
Photographing the spectra of weak (distant) sources to measure red shifts requires favorable observing conditions and lengthy exposure times even with the use of the largest telescopes and the most sensitive plates. Shifts of z ≈ 0.2, the corresponding velocities ν ≈ 60,000 km/sec, and a distance greater than 1 billion parsecs have been reliably measured for the galaxies. Hubble’s law at such velocities and distances is used in the simplest form (the error is of the order of 10 percent, that is, the same as the error in determining H). Quasars are on the average 100 times brighter than galaxies and, consequently, can be observed at distances ten times as great (if space is Euclidean). In fact, z ≈ 2 and greater have been recorded for quasars. For shifts of z = 2 the velocity is ν ≈ 0.8 • c = 240,000 km/sec. At such velocities the specific cosmological effects of nonstationariness and space-time curvature are greatly in evidence. In particular, the concept of a unique well-defined distance (one of the distances—the distance obtained from the red shift—is evidently r = v/H = 4.5 billion parsecs) becomes inapplicable here. The red shift attests to the expansion of all parts of the universe accessible to observation. This phenomenon is usually called the expansion of the (astronomical) universe.
Gravitational red shift. Gravitational red shift is a consequence of time dilatation caused by a gravitational field (an effect of the general theory of relativity). This phenomenon (also called the Einstein shift or generalized Doppler effect) was predicted by A. Einstein in 1911 and was first observed in 1919 in solar emission and subsequently in the emission of other stars.
It is customary to characterize the gravitational red shift by a nominal velocity v, formally calculated from the same formulas as in the case of cosmological red shifts. The values of the nominal velocity are ν = 0.6 km/sec for the sun and ν = 20 km/sec for the dense star Sirius B. The red shift caused by the earth’s gravitational field, which proved to be very small (v = 7.5 × 10−5 cm/sec), was first successfully measured in 1959 by the Môssbauer effect. In certain cases (for example, in gravitational collapse), both types of red shift (as additive effects) should be observed
No comments:
Post a Comment